AI Fashion App
We explored two fundamentally different approaches to digital clothing try-on. Our mission was to investigate both image manipulation and 3D mesh-based solutions, each serving distinct use cases in the virtual fashion industry.
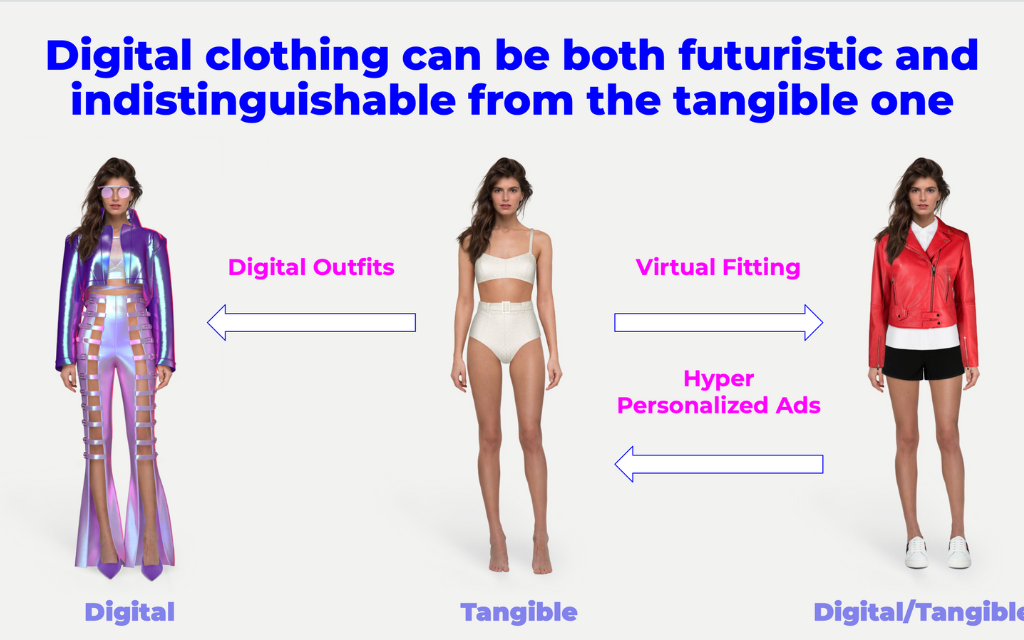
We explored two fundamentally different approaches to digital clothing try-on. Our mission was to investigate both image manipulation and 3D mesh-based solutions, each serving distinct use cases in the virtual fashion industry.
Image-Based Try-On Approach
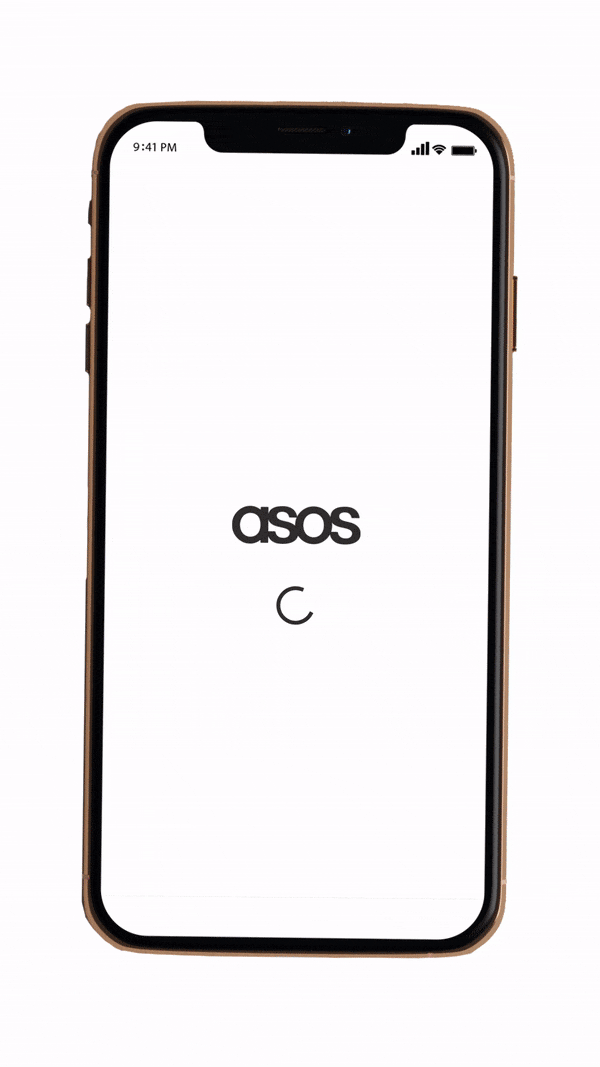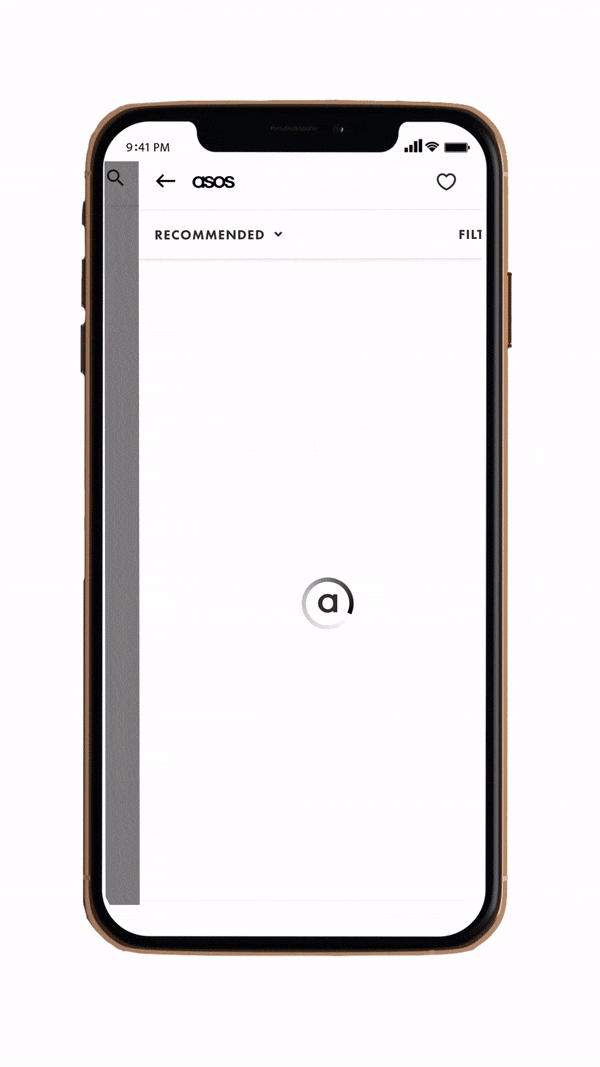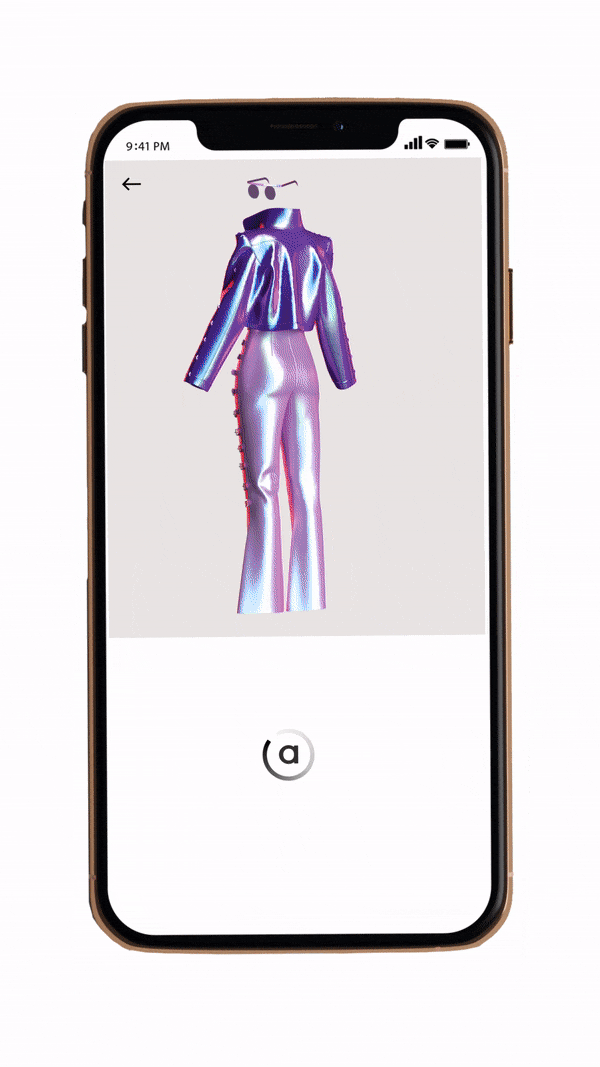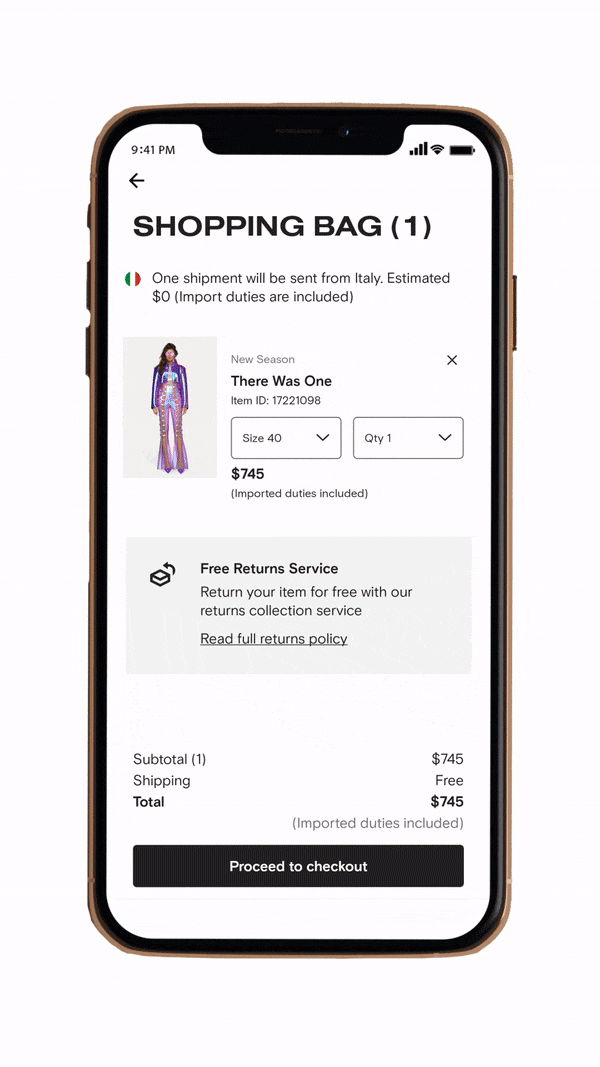
Our first approach focused on achieving visually perfect try-on results through sophisticated image manipulation techniques. We implemented BipartGraph, a bipartite graph network that establishes dense correspondences between clothing and body regions.
The core BipartGraph formulation can be expressed as:
\[\mathcal{G} = \{(\mathcal{V}_c \cup \mathcal{V}_b, \mathcal{E}), \mathcal{A}\}\]where $\mathcal{V}_c$ represents clothing nodes, $\mathcal{V}_b$ represents body nodes, and $\mathcal{A}$ is the adjacency tensor.
Human Parsing and Segmentation

For precise human parsing, we utilized SCHP (Self-Correction Human Parsing) with a novel hierarchical correction mechanism:
\[P_{t+1} = \text{SoftMax}(f(P_t, F) + P_t)\]where $P_t$ represents parsing results at stage $t$, and $F$ are deep features extracted through HRNet.
The hierarchical feature fusion is defined as:
\[Y^h = \sum_{l=1}^L w_l * X^l * M^l\]where $M^l$ represents attention masks at different resolutions.
Diffusion-Based Image Generation
We implemented Stable Diffusion with custom conditioning for clothing synthesis. The diffusion process follows:
\[q(x_t|x_0) = \mathcal{N}(x_t; \sqrt{\bar{\alpha}_t}x_0, (1-\bar{\alpha}_t)I)\]The reverse process is guided by:
\[p_\theta(x_{t-1}|x_t) = \mathcal{N}(x_{t-1}; \mu_\theta(x_t, t), \Sigma_\theta(x_t, t))\]Style Transfer and Refinement

For style preservation, we employed AdaIN (Adaptive Instance Normalization):
\[\text{AdaIN}(x, y) = \sigma(y)(\frac{x - \mu(x)}{\sigma(x)}) + \mu(y)\]This was enhanced with SPADE (Spatially-Adaptive Normalization) for spatial awareness:
\[\gamma_{c,y,x}(s) \frac{h_{c,y,x} - \mu_c}{\sigma_c} + \beta_{c,y,x}(s)\]3D Mesh-Based Approach
Our second approach focused on physical accuracy through detailed 3D modeling and simulation. We implemented SMPL-X, an expressive parametric body model.
Body Shape Estimation
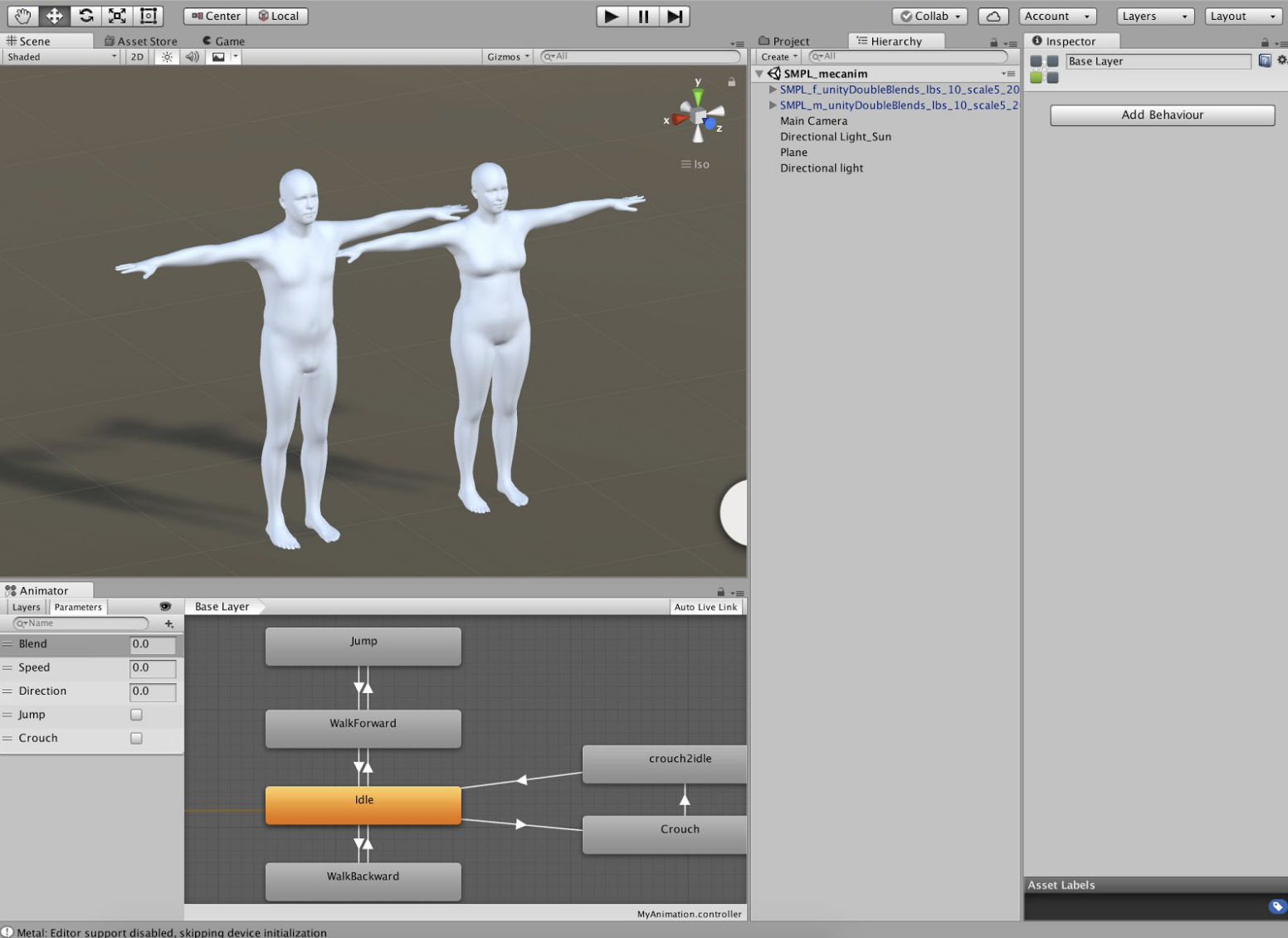
The SMPL-X model defines body shape through a differentiable function:
\[M(\beta, \theta, \psi) = W(T_P(\beta, \theta, \psi), J(\beta), \theta, \mathcal{W})\]where:
- $\beta$ represents shape parameters
- $\theta$ represents pose parameters
- $\psi$ represents expression parameters
- $W$ is the skinning function
We enhanced this with ICON (Implicit Clothed Humans Obtained from Normals) for better surface detail:
\[f_\theta: (x, z, c) \mapsto (s, n)\]where $s$ is the occupancy value and $n$ is the predicted surface normal.
Garment Modeling
For garment simulation, we implemented POP (Physics-based Optimization of Patterns). The physical simulation follows:
\[M\ddot{x} + C\dot{x} + K(x-x_0) = f_{ext}\]where:
- $M$ is the mass matrix
- $C$ is the damping matrix
- $K$ is the stiffness matrix
- $x_0$ is the rest pose
- $f_{ext}$ represents external forces
Contact Handling
We utilized SDF-based Contact Handling for realistic cloth-body interaction:
\[E_{contact} = \sum_{p \in \mathcal{P}} w_p \max(0, -\phi(p))^2\]where $\phi(p)$ is the signed distance function at point $p$.